Задача № 1. При каком наименьшем натуральном N>1 число (N³-N) делится на 2002?

Задача № 2. Даны 10 чисел. Какое наибольшее количество попарных сумм этих чисел может быть нечётными числами?

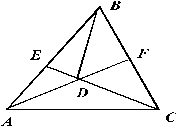
Задача № 3. AF - медиана треугольника ABC, D - ее середина. E - точка пересечения прямой CD со стороной AB. Оказалось, что BD=BF=CF. Докажите, что AE=DE.

Задача № 4. Депутаты городской думы делили дополнительные доходы бюджета. Первый лоббист выбил 1000 долларов и 1/10 оставшихся доходов, второй - 2000 долларов и 1/10 остатка, и так далее. После этого оказалось, что все лоббисты поделили доходы поровну. Сколько было лоббистов? (Лобби - группа представителей экономически сильных структур, оказывающих влияние на государственную политику. Лоббист - человек, принадлежащий к лобби.)

Задача № 5. Доска 10×10 была выложена плитками 2×2 и 4×1. Доказать, что если одну плитку 2×2 заменить плиткой 4×1, то снова выложить доску плитками не удастся.

Задача № 6. На гранях кубика расставлены числа от 1 до 6. Кубик бросила сначала Ксюша, потом - Оля. В первый раз сумма цифр на четырёх боковых гранях оказалась равна 12, во второй - 15. Затем бросил кубик Рома: на верхней грани кубика оказалась тройка. А какая цифра была при этом на нижней грани?

Задача № 7. В некоторой компании более 10 человек, и у каждого количество знакомых делится на 10. Докажите, что есть хотя бы 11 человек с одинаковым количеством знакомых.